Integración Numérica y Aproximación de Áreas
La integración numérica es una técnica que permite aproximar el valor de una integral definida cuando su cálculo analítico es complicado o imposible. En lugar de obtener un valor exacto, se estima el área bajo una curva dividiendo el intervalo de integración en partes más simples y sumando las áreas correspondientes. Esta técnica es ampliamente utilizada en física, ingeniería, economía y otras ciencias aplicadas.
Existen varios métodos de integración numérica, siendo los más comunes los métodos de rectángulo y el método del trapecio.
El método de rectángulo consiste en dividir el intervalo
en n subintervalos de igual tamaño
y construir rectángulos cuya altura se obtiene del valor de la función en el extremo izquierdo, derecho o punto medio de cada subintervalo. La suma de las áreas de estos rectángulos proporciona una aproximación del área bajo la curva. Por ejemplo, para aproximar el área bajo
de 0 a 2 usando 4 rectángulos por el método izquierdo, se calcula
y se suman las áreas:
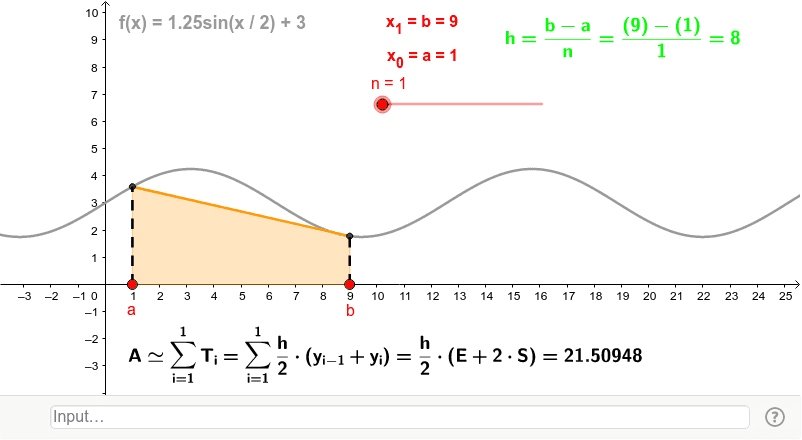
El método del trapecio mejora la precisión al aproximar cada subintervalo mediante un trapecio en lugar de un rectángulo. Para este método, se divide el intervalo en
n subintervalos y se aplica la fórmula:
Por ejemplo, aproximando
entre 1 y 3 con 4 subintervalos, se obtiene un área aproximada de 14.
En general, aumentar el número de subintervalos mejora la aproximación tanto en el método de rectángulo como en el del trapecio. El método del trapecio suele ser más preciso que el de rectángulo para el mismo número de subintervalos. Estas técnicas permiten estimar áreas bajo curvas, volúmenes o acumulaciones de magnitudes cuando no es posible realizar la integración de manera exacta.