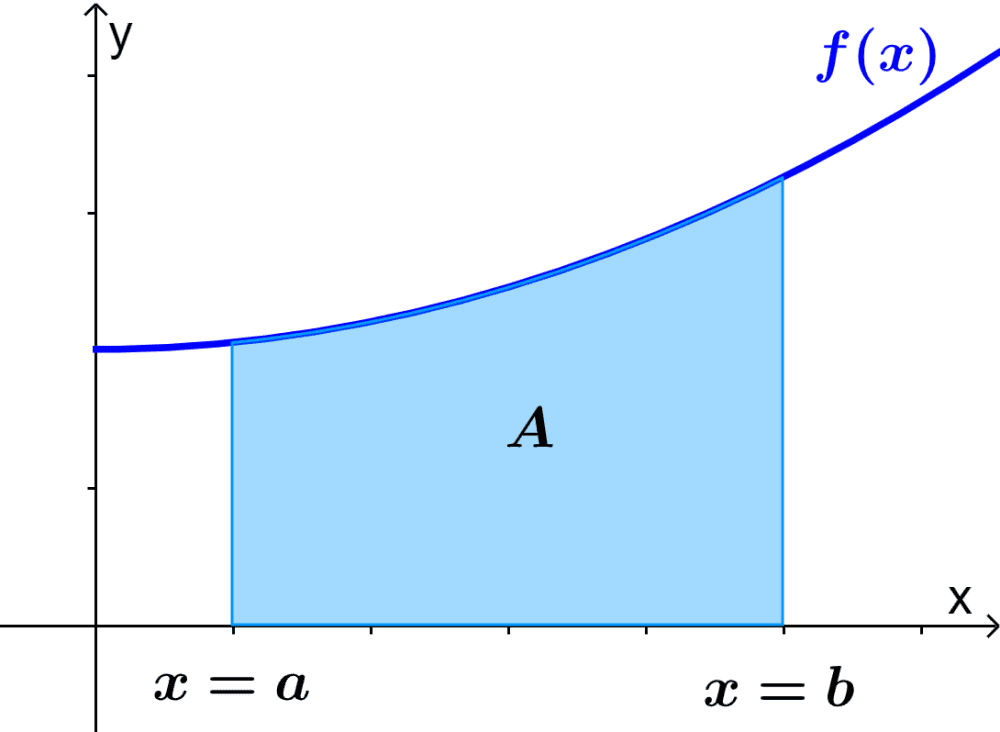
Área Bajo una Curva e Integral Definida
El área bajo una curva
entre dos puntos
y
se calcula mediante la integral definida, que permite sumar infinitesimales rectángulos bajo la gráfica de la función. Formalmente, se expresa como:
Si la función se encuentra por encima del eje x, el área es positiva; si cruza el eje, los valores por debajo del eje se consideran negativos. La integral definida también representa la acumulación de cantidades variables, como desplazamientos, trabajo o volumen.
Para calcular el área bajo la curva se siguen estos pasos:
-
Identificar la función f(x) y los límites a y b
-
Determinar si la función es positiva o negativa en el intervalo.
-
Calcular la integral definida usando la primitiva
de
-
Evaluar
según el Teorema Fundamental del Cálculo.
Ejemplo 1: Calcular el área bajo
entre
y
Ejemplo 2: Calcular
En ambos ejemplos se observa cómo la integral definida permite determinar el área bajo la curva y cómo los valores de la función sobre el eje x afectan el resultado.